Mathematics

Matematik

M=Matte

·         http://www.webbmatte.se/choose_language/svenska/sv.php flera övningar i matte

·         https://www.matteboken.se/  flera övningar i matte

·         https://www.mathsisfun.com/  Blandade roliga övningar i matte

·         https://www.mathsisfun.com/games/rayray-game.html övning i logiskt tänkande

·         http://www.kunskapshubben.se/  Multiplikation mm

·         http://www.mattesmedjan.se/multix/  Multiplikationsövning

NUMBERS (link)
Number Sense (link)
Khan Academy ( link)
Place Value of Numbers (Link)
Multiplication Tables
Multiplication Tables

Time and Dates

The children will have a test on the 23rd of January, 2019. They  are to revise Chapter 7 and 8 of Mattebogren 5B. They are  also to read page 63 and 89. They can train on Page 153-154 (Only sums with Fractions and Percentage). Worksheets were also issued for Fractions and Percentage. They should ensure that they have certainty in solving the problems in the worksheets too.
in those worksheets.

N.B
This plan is subject to adjustment or change depending on circumstances at school.

Plan for -2019 Spring Term

Week	Class Work	Homework
2	Intro to Geometry Pg.126-127, 5B	Worksheet
3	Revision Fractions and Percentage	Revision for Test Fractions and Percentage
4	Test (23/1-2019)Fractions and Percentage pg.135-136 (5B)	Pg. 128-130 (Geometry) 5B
5	131-132, 133-134 (Geometry)	Pg.140-141 (Geometry)
6	Pg 137-138, 139 &142(Geometry)	Pg 143-145 (Geometry)
7	146-147, 15-151(Geometry)	147-148 (Geometry)
8	Workshheet/programmering	Worksheet/programmering
9	Winter Sport Break
10	104-105,106-107,108-108                   (Vikt och volym)	Pg.100-103  ( Vikt och volym)
11	110-111, 116,117-118                    (Vikt och volym)	112-114,      (Vikt och volym)
12	122-123, 124, 126,127            Vikt och volym	119-121         (Vikt och volym)
13	Revision	Revision
14	Test Geometry+Vikt och volym Onsdag (3/4-2019)	Test Geometry+Vikt och volym
15	Programming	Programming
16	Easter	Holidays
17	Temperatur och Diagram 134-135,136-137,138	130-133
18	Temperatur och Diagram	142-144
19	Temperatur och Diagram 138-139,140-141	145-148
20	Temperatur och Diagram  149, 152, 153	Completing unaccomplished work
21	Repetition/ Test
22	Programming
23	Känguru Matematik

There are many special symbols used in Geometry. Here is a short reference for you:

Geometric Symbols

Congruent and Similar

• Congruent Shapes
• Similar Shapes

Angles

Types of Angles

Acute Angles

Right Angles

Obtuse Angles

Straight Angle

Reflex Angles

Full Rotation

Degrees (Angle) Radians Congruent Angles Parallel Lines and Pairs of Angles Transversal Adjacent Angles A Triangle Has 180° Supplementary Angles Complementary Angles

Angles Around a Point Angles on a Straight Line Interior Angles Exterior Angles Interior Angles of Polygons Exterior Angles of Polygons

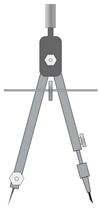Using Drafting Tools 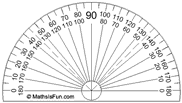Geometric Constructions Using the Protractor Using the Drafting Triangle and Ruler Using a Ruler and Compass

Transformations and Symmetry

Transformations:

• Rotation 
• Reflection 
• Translation 
• Resizing

Symmetry:

• Reflection Symmetry
• Rotational Symmetry
• Point Symmetry
• Lines of Symmetry of Plane Shapes

• Symmetry Artist

• Activity: Symmetry of Shapes
• Activity: Make a Mandala
• Activity: Coloring (The Four Color Theorem)

• Tessellations
• Tessellation Artist

Coordinates

• Cartesian Coordinates
• Interactive Cartesian Coordinates
• Hit the Coordinate Game

W

Week	Class Work	Homework
35	9-10, 11-12, 13-14 Tal (Number Sense)	16-18 Tal (Number Sense)
36	19-20, 22-23,29-29 Tal (Number Sense)	24-27 Tal (Number Sense)
37	30-31, 32-33, 38-39 (Tal)	34-36 Tal (Number Sense)
38	74-75, 80-81, 82-83( Decimal Tal)	76-79 (Decimal Tal)
39	84-85, 86-89,92-93 (Decimal Tal)	Page 88-91  (Decimal Tal)
40	14,15,16,17,18,19( Tal)	Page 27-30
41	31-32, 33&36, 37 (Decimal Tal 5B)	94-97 (Decimal Tal 5B)
42	98-99,104-105,106& and 108(Decimal Tal 5B)	100-103(Decimal Tal 5B)
43	112-113,114-115, 116-117(Decimal Tal 5B)	108-111(Decimal Tal 5B)
44
45	120  122 and 123	Revision
46	Repetition Test Programming (Page 44-45, 46-47, 48-49) Fractions)	Valfrit code .org eller scratch Page 40 -43 (Fractions)
47	Pg.50-51, 58-61 (Fractions)	Pg 53-56 (Fractions)
48	Page 62& 64-65 F Fractions)	68-70 (Percentage)
49	71-72, 73-74, 75-76 (Percentage)	77-80 (Percentage)
50	81-82, 83-84,90-91 (Percentage)	86-88 (Percentage)
51	Programming	Programming
52

Week	Class Work	Homework
35	9-10, 11-12, 13-14 Tal (Number Sense)	16-18 Tal (Number Sense)
36	19-20, 22-23,29-29 Tal (Number Sense)	24-27 Tal (Number Sense)
37	30-31, 32-33, 38-39 (Tal)	34-36 Tal (Number Sense)
38	74-75, 80-81, 82-83( Decimal Tal)	76-79 (Decimal Tal)
39	84-85, 86-89,92-93 (Decimal Tal)	Page 88-91  (Decimal Tal)
40	14,15,16,17,18,19( Tal)	Page 27-30
41	31-32, 33&36, 37 (Decimal Tal 5B)	94-97 (Decimal Tal 5B)
42	98-99,104-105,106& and 108(Decimal Tal 5B)	100-103(Decimal Tal 5B)
43	112-113,114-115, 116-117(Decimal Tal 5B)	108-111(Decimal Tal 5B)
44
45	120  122 and 123	Revision
46	Repetition Test
47
48
49
50
51
52

Update plan for Mathematics

Week	Class Work	Class Work	Homework
2	106-107 (M&D)	108 and 113 (M&D)	Page 110-112(M&D)
3	114-115(M&D)	121-123 (M&D) 4A	Page 116-119(M&D)
4	124-125    4A (M&D)	130-134 M&D   4A (M&D)	Page 128-129   4A  (M&D)
5	122-123 4b(M&D)	126-127 4b(M&D)	Page 128-129 4b (M&D)
6	134-135 4b M&D	141-143 4b(M&D)	Page 138-140 4b
7	136-137 4a statistics	142-144   4a statistics	Page 138-141 4a statistics
8	145-147 4a statistics	155-157 4a statistics	148-150 4a statistics
9
10	151-152 Statistics 4a	153 Revision	Revision (M&D) and statistics
11	Revision/ Intro Time	Test M&D +Statistics	10-144b   Time
12	8-9,15-16 4b        Time	17-18, 24-25 4b    Time	21-23 4b   Time
13	26-27, 30&324b   Time	33 Revision      Time	27-29 4b   Time
14
15	Fractions 4b  94-96,97-99	Fractions 4b 104-106	Fractions 4b 100-103
16	Fractions 4b 108-109,	Fractions 4b 114-115	Fractions 4b 110-112
17	Fractions 4b 113 and 116	Fractions 4b 118-119	Fractions 4b 148-149
18	Fractions 4b Revision	Fractions 4b Revision	Fractions 4b  Revision
19	Revision	Test (Time and Fractions) on 3rd May.

20	Geometry 4b Angles,enlargement,scale 68-69,  74-75		Geometry 4b Angles,enlargement,scale 76-77	Geometry 4b Angles, enlargement, scale   pg 70-73
21		Geometry 4b Angles, enlargement, scale 84-85, 86-87	Geometry 4b Angles, enlargement, scale 88	Geometry 4b Angles, enlargement, scale 80-83
22		Geometry 4b Angles, enlargement, scale 89-90	Page 135-140	4b 141-144
23		Revision	Revision End of Term	Revision End Of Term
23

Week	Class Work	Class Work	Homework
2	106-107 (M&D)	108 and 113 (M&D)	Page 110-112(M&D)
3	114-115(M&D)	121-123 (M&D) 4A	Page 116-119(M&D)
4	124-125    4A (M&D)	130-134 M&D   4A (M&D)	Page 128-129   4A  (M&D)
5	122-123 4b(M&D)	126-127 4b(M&D)	Page 128-129 4b (M&D)
6	134-135 4b M&D	141-143 4b(M&D)	Page 138-140 4b
7	136-137 4a statistics	142-144   4a statistics	Page 138-141 4a statistics
8	145-147 4a statistics	155-157 4a statistics	148-150 4a statistics
9

Qualitative vs Quantitative

Data can be qualitative or quantitative.

• Qualitative data is descriptive information (it describes something)
• Quantitative data is numerical information (numbers)

Bar Graphs

A Bar Graph (also called Bar Chart) is a graphical display of data using bars of different heights.

Imagine you just did a survey of your friends to find which kind of movie they liked best:

Table: Favorite Type of Movie
Comedy	Action	Romance	Drama	SciFi
4	5	6	1	4

We can show that on a bar graph like this:

It is a really good way to show relative sizes: we can see which types of movie are most liked, and which are least liked, at a glance.
We can use bar graphs to show the relative sizes of many things, such as what type of car people have, how many customers a shop has on different days and so on.

Example: Nicest Fruit

A survey of 145 people asked them "Which is the nicest fruit?":

Fruit:	Apple	Orange	Banana	Kiwifruit	Blueberry	Grapes
People:	35	30	10	25	40	5

And here is the bar graph:

That group of people think Blueberries are the nicest.
Bar Graphs can also be Horizontal, like this:

Example: Student Grades

In a recent test, this many students got these grades:

Grade:	A	B	C	D
Students:	4	12	10	2

And here is the bar graph:

You can create graphs like that using our Data Graphs (Bar, Line and Pie) page.

Histograms vs Bar Graphs

Bar Graphs are good when your data is in categories (such as "Comedy", "Drama", etc).
But when you have continuous data (such as a person's height) then use a Histogram.
It is best to leave gaps between the bars of a Bar Graph, so it doesn't look like a Histogram.

Line Graph: a graph that shows information that is connected in some way (such as change over time)
You are learning facts about dogs, and each day you do a short test to see how good you are. These are the results:

Table: Facts I got Correct
Day 1	Day 2	Day 3	Day 4
3	4	12	15

And here is the same data as a Line Graph:

You seem to be improving!

Making Line Graphs

You can create graphs like that using the Data Graphs (Bar, Line and Pie) page.
Or you can draw it yourself!

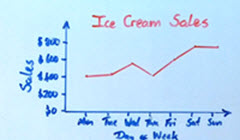
Example: Ice Cream Sales

Table: Ice Cream Sales
Mon	Tue	Wed	Thu	Fri	Sat	Sun
$410	$440	$550	$420	$610	$790	$770

Let's make the vertical scale go from $0 to $800, with tick marks every $200

Draw a vertical scale with tick marks

Label the tick marks, and give the scale a label

Draw a horizontal scale with tick marks and labels

Put a dot for each data value

Connect the dots and give the graph a title

Important! Make sure to have:

• A Title
• Vertical scale with tick marks and labels
• Horizontal scale with tick marks and labels
• Data points connected by lines

• Frequency

  Frequency is how often something occurs.
  
  

  Example: Sam played football on:

  • Saturday Morning,
  • Saturday Afternoon
  • Thursday Afternoon

  The frequency was 2 on Saturday, 1 on Thursday and 3 for the whole week.

  Frequency Distribution

  By counting frequencies we can make a Frequency Distribution table.
  

  Example: Goals

  Sam's team has scored the following numbers of goals in recent games
  

  2, 3, 1, 2, 1, 3, 2, 3, 4, 5, 4, 2, 2, 3

  Sam put the numbers in order, then added up:
  

  

  • how often 1 occurs (2 times),
  • how often 2 occurs (5 times),
  • etc,

  and wrote them down as a Frequency Distribution table.
  From the table we can see interesting things such as
  

  • getting 2 goals happens most often
  • only once did they get 5 goals
  This is the definition:
  
  Frequency Distribution: values and their frequency (how often each value occurs).
  Here is another example:
  

  Example: Newspapers

  These are the numbers of newspapers sold at a local shop over the last 10 days:
  

  22, 20, 18, 23, 20, 25, 22, 20, 18, 20

  Let us count how many of each number there is:
  

  Papers Sold	Frequency
  18	2
  19	0
  20	4
  21	0
  22	2
  23	1
  24	0
  25	1

  It is also possible to group the values. Here they are grouped in 5s:
  

  Papers Sold	Frequency
  15-19	2
  20-24	7
  25-29	1

  (Learn more about Grouped Frequency Distributions)

  Graphs

  After creating a Frequency Distribution table you might like to make a Bar Graph or a Pie Chart using the Data Graphs (Bar, Line and Pie) page.
  
  

För kommande Veckor

Klockor ser vi överallt. Klockor bestämmer när vi måste lägga oss, när nästa lektion börjar och när skoldagen är slut.

Detta är mycket bra att öva på:

• 1 år = 52 veckor
• 1 år = 12 månader
• 1 år = 365 dagar
• 1 kvartal = 3 månader

• 1 vecka = 7 dagar
• 1 dag = 24 timmar
• 1 timme = 60 minuter

När du är klar med geometri ska du

• Känna till något om hur man mätte sträcker förr
• Kunna mätta och rita sträckor
• Kunna uppskatta och mäta längd
• Kunna växla mellan olika längdenheter
• Känna till egenskaper och namnet på några geometriska objekt
• Kunna rita rektanglar med givna mått
• Kunna räkna ut figurers omkrets

Detta är mycket bra att öva på:

• 1 meter = 10 decimeter
• 1 decimeter = 10 centimeter
• 1 centimeter = 10 millimeter

För längre avstånd använder vi
1 kilometer = 1000 meter (kom ihåg att kilo betyder tusen)
1 mil = 10 kilometer

Volymer mäter vi oftast i liter. En vanlig vattenflaska kan innehålla ungefär en liter och en stor läskflaska innehåller ungefär en och en halv liter.

För mindre volymer (som en tekopp eller en liten ask) använder vi enheterna deciliter, centiliter och milliliter. De förkortas dl, cl och ml.

• 1 l = 10 dl
• 1 dl = 10 cl
• 1 cl = 10 ml

Kubikdecimeter är ett annat ord för liter men är inte lika vanligt i vardagen.

---

Skriv i milliliter (ml): 3 deciliter (dl) och 5 centiliter (cl).

3dl=3⋅10=30cl$$3dl=3\cdot 10=30cl$$

30+5=35cl$$30+5=35cl$$

35cl=35⋅10=350ml$$35cl=35\cdot 10=350ml$$

Svar: 350 milliliter

Begrepp

Sträcka
Meter
Centimeter
Millimeter
Kub
Kon
Cylinder
Tetraeder
Pyramid
Sida
sidoyta
Hörn
Kant
Längd
Bredd
omkrets
Line and Angle Terms :
A figure that is formed when two rays meet at a common endpoint.
where A is the common endpoint of the two rays.
 An angle can also be represented by three letters with the middle letter the common endpoint of the two rays and the first and last letters as points on each of the rays.
 For example: is angle A, is


Acute angle:
 An angle whose measure is less than 90-degrees,
 or right angle.
Obtuse angle: An angle whose measure is greater than 90-degrees,
or a right angle.
Right angle: An angle whose measure is exactly 90-degrees.
Straight angle: An angle whose measure is 180-degrees, which forms a straight line.
Rotational symmetry: A term describing a shape that remains unchanged when it is turned less than 360-degrees about a fixed Point


Square and Rectangle Terms :
Square :A closed figure with four equal sides and four equal (right) angles.
Rectangle: A closed figure with four sides, whose opposite sides are equal and with four equal (right) angles. Right angle: An angle whose measure is exactly 90-degrees.
Similar shapes:
Two shapes that have the exact same shape—corresponding angles that are congruent and corresponding sides that are proportional.
Congruence:
The relationship between two geometric shapes having the same size and shape (congruent shapes).
Quadrilateral Terms :
Any four-sided, closed figure.
Trapezoid: A quadrilateral with exactly one pair of parallel sides.
Parallelogram: A quadrilateral with opposite sides that are equal and parallel.
Rhombus: A parallelogram with four congruent sides.
Square: An equilateral and equiangular quadrilateral. (OR: A closed figure with four equal sides and four equal (right) angles.) Rectangle: A quadrilateral with all interior right angles.


Pyramid Terms :
 A simple, closed, three-dimensional shape formed by plane polygons.
Pyramid: A polyhedron that has one base and a set of edges that meet at a single point (apex) that is not in the base; all faces except the base MUST be a triangle; the base MAY be a triangle.
Triangular pyramid: A pyramid with a triangular base.
Square pyramid: A pyramid with a square base.
Vertex: The point where two rays forming an angle meet; the point where two sides of a polygon meet; or the point where three or more faces of a polygon meet.
Vertices: Plural of vertex.
Edge: The line of a three-dimensional shape where two plane faces meet. Face:
 One of the plane surfaces of a polyhedron bounded by edges. Base: The side of a shape used as its foundation; the face of a solid used as its foundation.
Apex: The point, off the base of a pyramid, where the triangular faces meet.
Net: A pattern that can be cut out, folded and glued together to make a three-dimensional model of a solid Point


More 2-D Shapes Polygon:
A simple closed shape composed of a finite number of line segments, each of which intersects exactly two of the other segments, one at each endpoint.
Pentagon:
A polygon with five sides. Regular pentagon: A polygon with five congruent sides and five congruent angles.
Hexagon:
A polygon with six sides. Regular hexagon: A polygon with six congruent sides and six congruent angles.
Octagon:
 A polygon of eight sides. Regular octagon: A polygon of eight congruent sides and eight congruent angles.


More 3-D Shapes Polyhedron:
A simple, closed, three-dimensional shape formed by plane polygons.
Cube:
A rectangular polyhedron composed of six congruent squares.
Triangular prism:
A polyhedron that has two congruent parallel triangular faces and a set of parallel edges that connect corresponding vertices of these two triangular faces.
Vertex: The point where two rays forming an angle meet; the point where two sides of a polygon meet; or the point where three or more faces of a polygon meet.
Vertices: Plural of vertex.
Edge: The line of a three-dimensional shape where two plane faces meet.


Pattern: A way that things are arranged so that whatever comes next can be predicted.
Fraction: Part of a whole, or part of a set. It can be expressed as a rational number over a rational number.
For example: 1/4. Equivalent fraction:
Different ways of naming the same fraction.
For example: 4/8 and 2/4 are both equivalent to 1/2.
Midpoint: A point that divides a line segment into two congruent line segments.

Arbetsätt
Tillverka egna linjalen
Arbeta par/grupp
Rita gemetriska figurer
Beskriva formerna kvadrat, rektangel, cirkel
kub, tetraeder, pyramid, klot, cylinder och kon
Beräkna area och omkrets

Under Constrction!








Homework week 35
 Matte Borgen  4A  page 13-15. To be  handed in on Friday week 35.

Bedömning
Problemlösning
Du ska:

• förstå frågan i en textuppgift
• använda olika  strategier när du löser ett problem
• tolka dina resultat och dra en slutsats
• avgöra om ett svar är rimligt
• lösa problem själv
• lösa problem i grupp

 Begrepp

 Du ska:

•  använda begreppen
•  beskriva begreppen
•  använda olika uttrycksformer för att beskriva begrepp
•  beskriva olika uttrycksformer för att beskriva begrepp
•  beskriva likheter och skillnader mellan begrepp
• visa samband mellan begrepp

Methoder

 Du ska

• :använda en skriftlig räknemetod som passar till uppgiften
•  välja och använda den metod som passar bäst för den uppgiften
•  använda en huvudräkningsmetod som är snabb och enkel
•  och använda passande räknesätt i en problemlösningsuppgift
•  använda miniräknare

 Resonemang
 Du ska :

• ställa och besvara frågor i grupp
•  motivera din lösning skriftligt
•  motivera din lösning muntligt
•  följa andra elevers förklaringar och bidra med ideer om hur en uppgift
• kan lösas
• första andra elevers förklaringar och bidra med egna ideer

 Kommunikation
 Du ska:

•  förklara vad som menas med olika begrepp
•  berätta för en kamrat hur du har löst en uppgift
•  redovisa dina uppgifter skriftligt så någon annan förstår vad
•  du menar
•  lyssna på en kamrats förklaring hur den e löst en uppgift
•  visa min lösning med bild och / eller symboler

Rest Under Construction!